C语言中的计算机基础

计算机如何计算

目前计算机都只能认识0和1，因此不管是在CPU的寄存器中、还是在内存中、硬盘中存储的都是0和1（晶体管的通断），并且计算机（CPU的ALU）是对0和1进行简单的加法（减法也会变成加法来进行运算，因为ALU只能做加法，这也引出了反码和补码）。

原码、反码、补码

理解原码、反码、补码这一篇就够了，写的很明白，主要内容如下：

原码是人类容易理解的

反码是解决计算机的问题，因为ALU单元只能进行加法，所以 $10-2$ 会被转换成 $10+(-2)$ 进行运算，但是如果都用原码进行运算的话结果会有问题，因此引出了反码。

补码是为了解决反码中0的表示有两种，即 $+0$ 和 $-0$ ，分别是 $0b00..00$ 和 $0b11..11$ ，对应十六进制就是 $0x00$ 和 $0xff$ 。而用反码的话，0的表示就只有 $0x00$ ， $0xff$ 表示 $-1$ 。

前面说了，计算机中存储的都是0和1，因此单纯来讲，这没有什么意义。只有当人类规定了某种协议，这些0和1才变得有意义，计算机才发挥出它无与伦比的作用。

举个例子，现在假设内存M=0x00000001处物理存储值为：0b00001111 (1B)。如果没有统一的规定，那么一千个哈姆雷特就有一千个看法，因此规定：

最高位为符号位，0为正、1为负
其余为组成有效数字位

因此M内存处的值表示+15，假若内存M处物理存储值为：0b10000011 (1B)，则其表示的值是-3（其实不是-3，因为计算机中的物理值是补码的形式，需要转换才能得到原码）。

物理存储值（物理值）：我自己定义的名词，定义为内存中真实的bit状态（和晶体管真实的物理通断一样）

但注意：计算机中的物理存储值是补码的形式（为什么用补码请看上面的链接），因此还需要转换才能得到原码，正数就不用转换。看下面的C语言代码：

void bin2num()
{
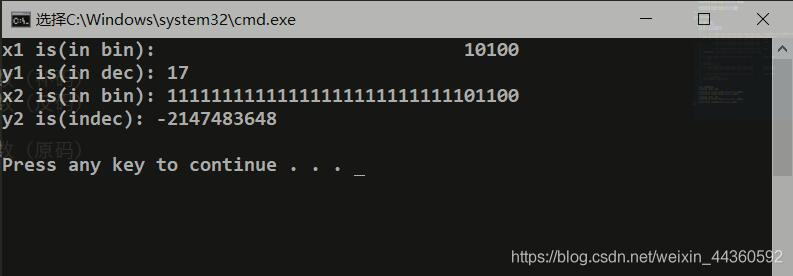
	int x1 = 20;			// 输出0000 ... 0000 0001 0100
	int x2 = -20;			// 输出1111 ... 1111 1110 1100
	int y1 = 0x00000011;	// %d输出20
	int y2 = 0x80000011;	// %d输出-2147483648
	/**
	 * x1 =  20 = 0000 0000 0000 0000 0000 0000 0001 0100	正数的原码、反码、补码都是一样
	 * 	因此printf("x1 is(in bin): %032s\n", str);会输出上面的二进制字符串
	 * x2 = -20 = 1000 0000 0000 0000 0000 0000 0001 0100	原码
	 * 			= 1111 1111 1111 1111 1111 1111 1110 1011	反码
	 * 			= 1111 1111 1111 1111 1111 1111 1110 1011
	 * 				+									1
	 * 			= 1111 1111 1111 1111 1111 1111 1110 1100	补码
	 * 	因此会输出：1111 1111 1111 1111 1111 1111 1110 1100
	 *
	 * y1 = 0000 0000 0000 0000 0000 0000 0001 0001			正数（补码就是原码）
	 * 	  = 16 + 1
	 * 	  = 17
	 * 	因此会输出：17
	 * y2 = 1000 0000 0000 0000 0000 0000 0001 0001			负数（补码）
	 * 	  = 1111 1111 1111 1111 1111 1111 1110 1110			负数（反码）
	 * 	  	+									  1
	 * 	  = 1111 1111 1111 1111 1111 1111 1110 1111			负数（原码）
	 * 	  = -2147483648
	 * 	因此会输出：-2147483648
	 */

	char str[32];
	itoa(x1, str, 2);
	printf("x1 is(in bin): %032s\n", str);
	printf("y1 is(in dec): %d\n", y1);
	itoa(x2, str, 2);
	printf("x2 is(in bin): %032s\n", str);
	printf("y2 is(indec): %d\n", y2);
}

学过C语言的都知道printf有控制字符，比如%d,%f,%s等，它们其实就是一种协议，规定物理存储值如何表示数据。

printf的隐患-click here

其实printf在被调用的时候会维护一个变量栈，比如printf("%d, %f\n", a, b);，执行这句话时，会有以下几步：

printf维护一个变量栈；
参数从右到左依次入栈（printf维护的变量栈）；
根据格式字符串format中的控制字符（如%d）依次出栈，遇到%d则从栈顶弹出4B数据，遇到%f则弹出8B数据（当然跟具体的平台有关，跟编译器也有关）；
假设当前遇到的是%d，然后从栈顶弹出4B的数据，假设物理值为0b00...11，则会在终端输出3，如果是0bffffffff，则会输出-1。

/**
 * 程序代码中的十六进制数内存中的体现是如何的？
 * @Author   CofCai
 * @DateTime 2020-11-29T10:34:19+0800
 */
void hexInProg()
{
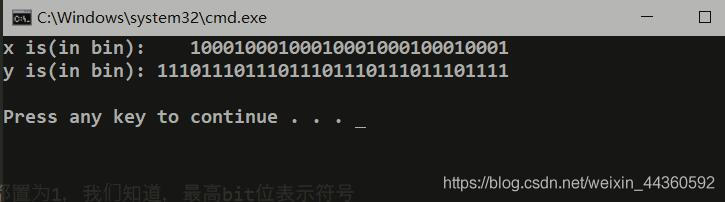
	int x = 0x11111111;
	int y = -0x11111111;	//所有位（包括符号位）取反加1
	char str[32];
	itoa(x, str, 2);
	printf("x is(in bin): %032s\n", str);
	itoa(y, str, 2);
	printf("y is(in bin): %032s\n", str);
}

进入内存改数据

/**
 * author:		CofCai
 * datatime:	2020-11-28 19:48:40
 * file description:
 *	 该文件主要是展示几个C语言能直接操控内存的例子
 */

#include <stdio.h>
#include <stdlib.h>

void BigOrLitEndian(void* para);
void changeNumByMem(void* para);

int main(int argc, char const *argv[])
{
	changeNumByMem(NULL);

	return 0;
}

void changeNumByMem(void* para)
{
	int a = 0x12345678;
	int pa;
	pa = (int)&a;
	printf("a is:0x%x\n", a);
	printf("a's addr is: 0x%x\n", pa);
	pa += 3;
	printf("pa is: 0x%x\n", pa);
	*((int*)pa) = 0xab;
	printf("now, a is: 0x%x\n", a);		//输出：0xab345678
	/** 
	 * 注意：我的电脑是小端模式，分析时要注意
	 * address:
	 * 		low						high
	 * 			78	56	34	12
	 * 		 	pa
	 * 		operation:pa += 3
	 * 		
	 * 		low						high
	 * 			78	56	34	12
	 * 						pa
	 * 		operation:*((int*)pa) = 0xab
	 * 		
	 * 		low						high
	 * 			78	56	34	ab
	 * 		 				pa
	 * 		output:0xab347856
	 */
	pa = (int)&a + 1;
	printf("pa is: 0x%x\n", pa);
	*((int*)pa) = 0xabcdef;
	printf("0x%x\n", a);				//输出：0xabcdef78

	pa = (int)&a + 2;
	printf("pa is: 0x%x\n", pa);
	*((char*)pa) = 0xee;				//输出：0xabee5678
	printf("0x%x\n", a);
}

/* 判断电脑的大小端 */
void BigOrLitEndian(void* para)
{
	int x = 0x12345678;
	int* px = malloc(sizeof(int)*1);
	px = &x;
	char* pch;
	pch = (char*)(px);
	if (*pch == 0x12) {
		printf("current PC is Big endian\n");
	} else if (*pch == 0x78) {
		printf("current PC is Little endian\n");
	} else {
		printf("0x%0x\n\n", *pch);
		printf("can't judge!\n");
	}
}

浮点数的表示

参考1-带例子

参考2-结合参考1好理解

浮点数由符号位S（占1bit）、阶码E、尾数M三部分组成，真实值为：

n = (-1)^S{\times}m{\times}2^e

规格化时，即当E的二进制位不全为0，也不全为1时，为规格化形式，此时：
$e = E-bias \\ m = \left|1.M\right|$
非规格化时，即当E的二进制位全部为0时，此时：
$e = 1 - bias \\ m = \left|0.M\right|$
$bias = 127(4B)$ （单精度：1+8+23）或 $bias = 1023(8B)$ （双精度：1+11+52）；
特殊数值：当E的二进制位全位1时为特殊数值
- 若此时M的二进制位全为0，则n表示无穷大（加上符号位就是正负无穷大）
- 若此时M的二进制位不全为0，则n表示 $Nan$ 。

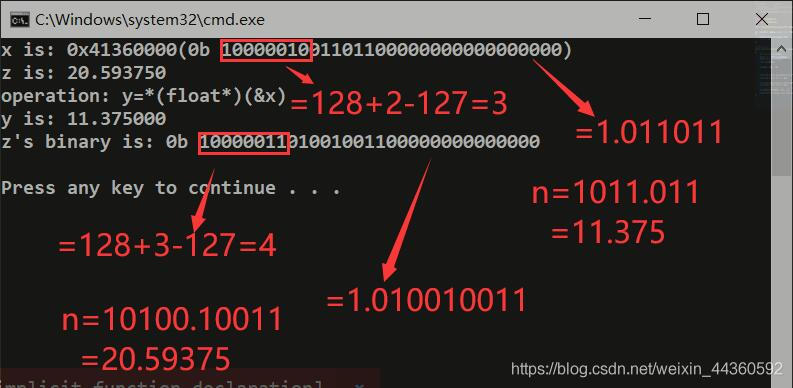
//链接中的例子
void int2floatInBinary(void* para)
{
	int x = 0x41360000;			//对应的二进制为：xxxx
	float y = *(float*)(&x);
	float z = 20.59375;
	char str[64];

	itoa(x, str, 2);
	printf("x is: 0x%x(0b%s)\n", x, str);
	printf("z is: %f\n", z);

	printf("operation: y=*(float*)(&x)\n");
	printf("y is: %f\n", y);
	// can't itoa((int)z, str, 2)
	itoa(*((int*)&z), str, 2);
	printf("z's binary is: 0b%s\n", str);
}

计算机如何计算

原码、反码、补码

进入内存改数据

浮点数的表示

感谢您的支持，我会继续努力的!