从各个名词的说起
FS,FT,LT、ZT、DTFT、DFS、DFT、FFT
先看这个一文弄懂DFT、DTFT、DFS的关系
另参考有道云笔记中的“从傅里叶级数到傅里叶变换”
先从图直观来看
x(t)及其傅里叶变换X(jw):
F(jw)=∫−∞+∞f(t)e−jωtdt(1)f(t)=2π1∫−∞+∞F(jw)ejωtdω(2)
- (1)频域某个点(把ω视为常数),由时域各个时间点的叠加组成。因为时域是连续的,所以频域某个频率成分(频率点)等于时域各个时间点的积分。
- (2)时域某个点(把t视为常数),由频域各个频率成分的叠加组成。因为频域是连续的,所以时域某个时间点等于频域各个频率成分(频率点)的积分。
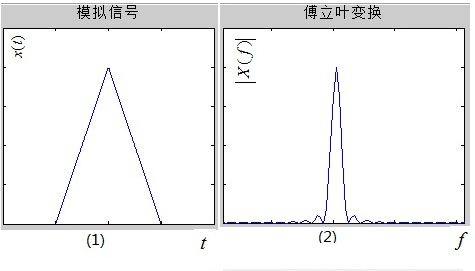
对时域采样进行离散化:

记住:周期冲激序列的傅里叶变换仍是周期冲激序列,强度和周期都是2π/T,时域相乘,等于频域卷积。得到离散的x(n)和连续的X(ejω)。
δT(t)=n=−∞∑+∞δ(t−nT)⟺ω0δω0(ω)=n=−∞∑+∞ω0δ(ω−nω0)ω0=T2π
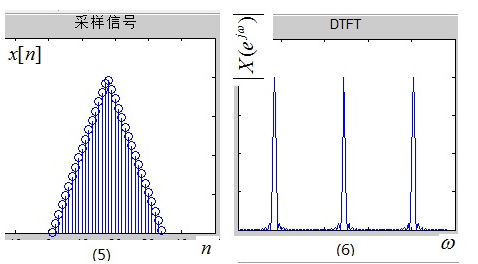
从结果可以发现,虽然时域被采样离散化了,但频域还是连续的,不利于计算机处理,所以我们对频域进行采样离散化。注意:从图5到图6就是DTFT。

同样,频域相乘等于时域卷积。从连续的X(ejω)得到离散的X(k)。注意:从x(n)到X(k)就是DFT,即从图5到图10。
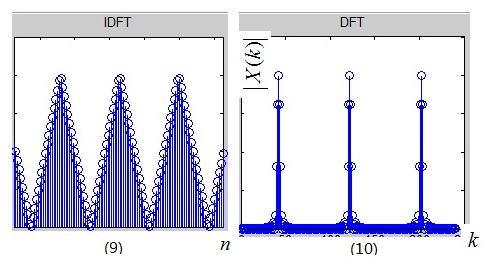
从图6到图10经过了离散化,所以横坐表也从ω变为了k,k也可以认为是频率。
各个变换的关系-图示:

- 非周期序列x(n)的N点DFT就是X(k)(即图10),但是k需满足0≤k≤N−1,即将k的取值限制在主值区间,这隐含X(k)是周期函数。
- 对x(n)周期化后,再求其DFS,结果其实就是DFT,只不过DFS的结果中对k没有要求。
- DFT的结果与选取的点数N有关,N越大,结果越精确。
- 可见,DFT只是为了计算机处理方便,在频率域对DTFT进行的采样并截取主值而已。有人可能疑惑,对图(10)进行IDFT,回到时域即图(9),它与原离散信号图(5)所示的x[n]不同呀,它是x[n]的周期性延拓!没错,因此你去查找一个IDFT的定义式,是不是对n的取值区间进行限制了呢?这一限制的含义就是,取该周期延拓序列的主值区间,即可还原x[n]!
长图:
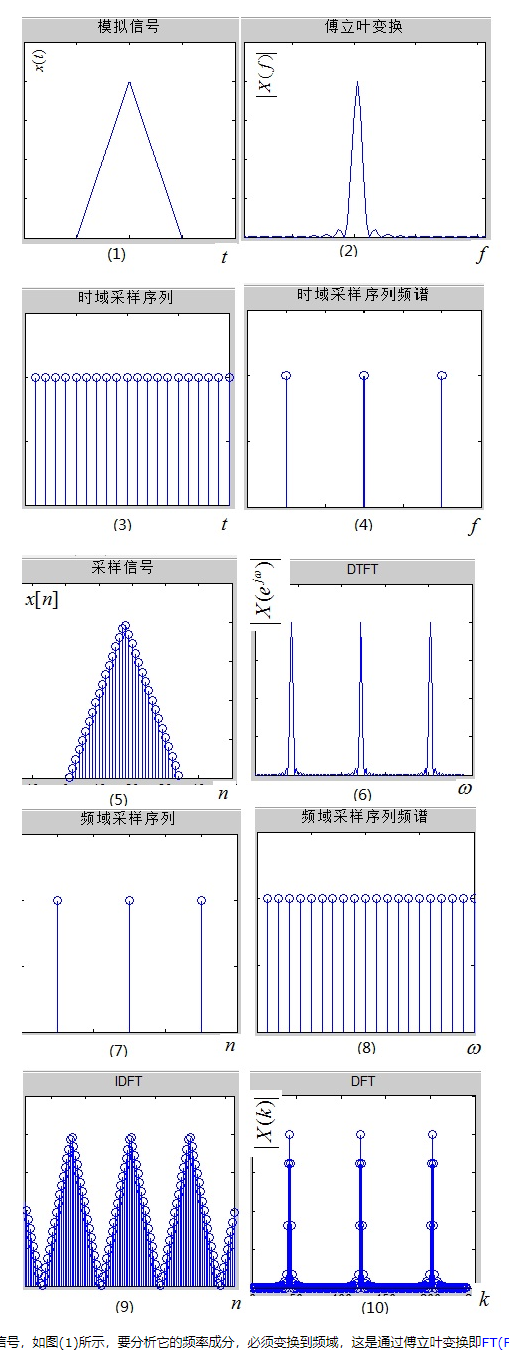
FS表示傅里叶级数
话说傅里叶大佬发现了任何一个周期函数都能用许多个正弦函数之和来表示,即
fT(t)=2a0+n=1∑∞(ancos(nω0t)+bnsin(nω0t))n=0,1,2,...其中an=T2∫t0t0+TfT(t)cos(nω0t)dtn=0,1,2,...bn=T2∫t0t0+TfT(t)sin(nω0t)dtn=0,1,2,...
或者写成指数形式:
fT(t)=n=−∞∑+∞Fnejnω0tω0=T2π(1)Fn=T1∫−2T2TfT(t)e−jnω0tdtn=0,±1,±2,...(2)
时频域变换解释:
- (1)时域某个时间点,由频域各个频率成分(nω0)的叠加组成。
- (2)频域某个频率成分的强度,由时域各个时间点的叠加组成(时域是连续的,所以是积分)。
但是对于非周期函数却不能展开成傅里叶级数,此时就演变出了傅里叶变换。
FT表示傅里叶变换
从FS到FT的推导就省略了,下面是结果:
f(t)=2π1∫−∞+∞∫−∞+∞f(t)e−jωtdtejωtdωF(jw)=∫−∞+∞f(t)e−jωtdt(1)f(t)=2π1∫−∞+∞F(jw)ejωtdω(2)
时频域变换解释:
- (2)时域某个时间点,由频域各个频率成分(ω)的叠加组成(频域是连续的,所以是积分)。
- (1)频域某个频率成分,由时域各个时间点的叠加组成(时域是连续的,所以是积分)。
FT能够将信号从时域搬到频域,便于分析;但还是不利于处理,因为计算机能够处理的都是数字信号,即是离散的,因此可以通过抽样在时域进行离散化。
上式表达式是有条件的,即f(t)满足绝对可积。然而连续周期信号并不满足,但是它可以展开成傅里叶级数,引入冲激函数后也可表示其傅里叶变换。
周期信号的傅里叶变换
周期信号不满足绝对可积的条件,但引入冲激函数后即可求得其傅里叶变换。
那么周期信号的FT是什么呢?
下面这个推导不是很好理解:

信号与系统书上的推导(比较好理解):
∵fT(t)=n=−∞∑∞Fnejnω0t,ω0=T2π∴FT(jw)=F[fT(t)]=F[n=−∞∑∞Fnejnω0t]=n=−∞∑∞FnF[ejnω0t]∵F[ejnω0t]=2πδ(ω−nω0)∴FT(jw)=2πn=−∞∑∞Fnδ(ω−nω0)
上式表明:周期信号的傅里叶变换由无穷多个出现在谐波频率nω0上的冲激函数组成,每一冲激的强度为傅里叶系数Fn乘上2π
单位周期冲激序列δT(t)的傅里叶变换是什么呢?

- 周期性冲激序列δT(t)的傅里叶系数Fn=1/T。

已知δT(t)=n=−∞∑∞δ(t−nT),ω0=T2π∵f(t)=δT(t)→Fn=T1∴F[δT(t)]=2πn=−∞∑∞Fnδ(ω−nω0)=T2πn=−∞∑∞δ(ω−nω0)=ω0n=−∞∑∞δ(ω−nω0)=ω0δω0(ω)
结论:周期为T的冲激序列的傅里叶变换也是周期冲激序列,其强度是ω0=T2π,其周期也是ω0。
DFTF表示离散时间傅里叶变换
重点是在于离散时间,即在时间域上是离散的,但其变换的结果在频域上依然是连续的。
∵xs(t)=x(t)δT(t)=x(t)n=−∞∑∞δ(t−nT)∴Xs(jω)=F[xs(t)]=∫−∞+∞x(t)n=−∞∑∞δ(t−nT)e−jωtdt=n=−∞∑∞∫−∞+∞x(t)δ(t−nT)e−jωtdt=n=−∞∑∞x(nT)e−jωnT∫−∞+∞δ(t−nT)dt=n=−∞∑∞x(nT)e−jωnT
令T=1,则变为:
Xs(jω)=n=−∞∑∞x(n)e−jωn或X(ejω)=n=−∞∑∞x(n)e−jωn
不管是jω,ejω,还是ejΩ,最终的自变量都是ω(ω=ΩT,T为采样周期)。
数字信号处理书上的定义:
X(ejω)=F[x(n)]=n=−∞∑∞x(n)e−jωn(1)x(n)=F−[X(ejω)]=2π1∫−ππX(ejω)ejωndω(2)
时频域变换解释:
- (1)频域某个频率成分,由时域各个序列点的叠加组成(时域是离散的,所以是求和)。
- (2)时域某个序列点,由频域各个频率成分(ω)的叠加组成(频域是连续的,所以是积分)。

上式表达式是有条件的,即x(n)满足绝对可和。然而离散周期信号并不满足,但是它可以展开成离散傅里叶级数,如下。另外,可以发现DTFT的结果中ω仍然是连续的,不利于计算机处理。
DFS表示离散傅里叶级数
设x(n)是以N为周期的周期序列,则其可以展开成离散傅里叶级数。
推导:
我们知道x(n)的基波成分为e1(n)=a1ejN2πn,k次谐波成分为ek(n)=akejN2πk⋅n。又因为ej((2π/N)(k+N)n=ej((2π/N)kn,所以离散傅里叶级数中只有N个独立的谐波成分,展开成傅里叶级数时,只能取k=0→N−1的N个独立的谐波分量,k=0表示直流分量。因此,x(n)展开成离散傅里叶级数如下:
x(n)=k=0∑N−1akejN2πkn
为求系数ak,将上式两边乘以e−jN2πmn,并对n在一个周期N中求和,即:

定义为:
X(k)=DFS[x(n)]=n=0∑N−1x(n)e−jN2πkn(1)x(n)=IDFS[X(k)]=N1k=0∑N−1X(k)ejN2πkn(2)
时频域变换解释:
- (1)频域某个频率成分(ω=N2πk),由时域各个序列点的叠加组成(时域是离散的,所以是求和)。
- (2)时域某个序列点,由频域各个频率成分(ω=N2πk)的叠加组成(频域是离散的,所以是求和)。
- 注意:
- (1)的结果对k没有限制,即k可以取从−∞到+∞的任何整数,对应的频率就是N2πk;但是求和时只对n从0到N-1的序列点求和。
- (2)的结果对n没有限制,即n可以取从−∞到+∞的任何整数,对应的时间就是n。但是求和时只对k从0到N-1的频率成分求和。
- 这是DFS与DFT最大的区别,也是联系。
x(n)是以N为周期的周期序列,那为什么频域的某个频率成分只等于一个周期内(n=0→n=N−1)的叠加呢?其它序列点不贡献频率成分吗?详看书上推导(主要原因是其独立的频率成分就只有N个)。
和FS对比理解:
fT(t)=n=−∞∑+∞Fnejnω0t(1)Fn=T1∫−2T2TfT(t)e−jnω0tdt(2)
DFT表示离散傅里叶变换
因为DTFT的结果在频域上依然是连续的,不利于计算机处理,所以对频域进行采样离散化。x(n)是一个长度为M的有限长序列,则定义x(n)的N点离散傅里叶变换为:

书上DFT的定义:
X(k)=DFT[x(n)]=n=0∑N−1x(n)WNknk=0,1,...,N−1x(n)=IDFT[X(k)]=N1k=0∑N−1X(K)WN−knn=0,1,...,N−1WN=e−jN2π
其实就是:
∵WN=e−jN2π∴X(k)=DFT[x(n)]=n=0∑N−1x(n)e−jN2πknk=0,1,...,N−1(1)x(n)=IDFT[X(k)]=k=0∑N−1X(K)ejN2πknn=0,1,...,N−1(2)
时频域变换解释:
- (1)频域某个频率成分(ω=N2πk),由时域各个序列点的叠加组成(时域是离散的,所以是求和)。
- (2)时域某个序列点,由频域各个频率成分(ω=N2πk)的叠加组成(频域是离散的,所以是求和)。
- 注意:
- (1)的结果对k有限制,即k只能取从0到N-1之间的整数,对应的频率就是N2πk;求和时也是只对n从0到N-1的序列点求和。
- (2)的结果对n有限制,即n只能取从0到N-1之间的整数,对应的时间/序列就是n。求和时也是只对k从0到N-1的频率成分求和。
- 这是DFS与DFT最大的区别,也是联系。
和DFS的区别:
X(k)=DFS[x(n)]=n=0∑N−1x(n)e−jN2πknx(n)=IDFS[X(k)]=N1n=0∑N−1X(k)ejN2πkn
不考虑其它的,DFS的表达式和DFT一模一样,只是DFT对k和n的取值有限定,DFT中对k和n的限定其实就是使其在主值区间,看这。
周期序列的傅里叶变换表达式
先前说过,周期信号不满足绝对可积,所以无法通过FT求得其傅里叶变换,但是引入冲激信号后可表示。周期序列也是一样的,不满足绝对可和,但通过展开成傅里叶级数,再引入冲激序列即可。如下:


还记得吗?前面我们推导了周期信号的傅里叶变换是由一系列在谐波处的冲激函数组成,其强度是傅里叶系数乘上2π;现在我们得到了复指数序列的傅里叶变换,其结果是在ω0+2πr(r为整数)处的单位冲激函数,强度为2π,周期序列的傅里叶变换是:
X(ejω)=F[x(n)]=k=0∑N−1N2πX(k)r=−∞∑∞δ(ω−N2πk−2πr)式中,K=0,1,2,...,N−1。如果让k在−∞到∞区间变换,上式可简化为X(ejω)=N2πk=−∞∑∞X(k)δ(ω−N2πk)式中X(k)=n=0∑N−1x(n)e−jN2πkn
FFT表示快速傅里叶变换
FFT其实就是DFT,只不过是利用DFT的某些性质,使得计算更加快速。
DFT与FT,ZT的关系
设序列x(n)的长度为M。
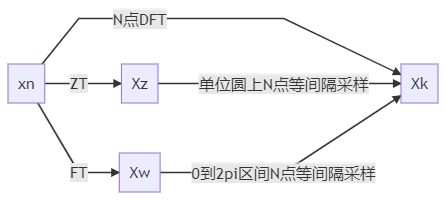
X(z)=ZT[x(n)]=n=0∑M−1x(n)z−n(1)X(ejω)=DTFT[x(n)]=n=0∑M−1x(n)e−jωn(2)X(k)=DFT[x(n)]N=n=0∑M−1x(n)WNkn=n=0∑M−1x(n)e−jN2πnkk=0,1,...,N−1(3)
-
序列x(n)的N点DFT-X(k)是x(n)的Z变换在单位圆上的N点等间隔采样;
X(k)=X(z)∣∣z=ejN2πkk=0,1,...,N−1
-
X(k)是x(n)的傅里叶变换X(ejω)在区间[0, 2π]上的N点等间隔采样;
X(k)=X(ejω)∣∣w=N2πkk=0,1,...,N−1

FT与LT的关系
因为并不是所有的信号都能傅里叶变换(需要满足绝对可积),所以可以乘上一个衰减因子e−δt,这样能使新构造的信号满足绝对可积,进而实现从时域变换到频域(此时是复频域)。因为e−jωte−δt=e−(δ+jω)t=e−st,s=δ+jω即为复频域,当δ为0时,即退化为傅里叶变换。
即LT变换是FT的推广,从频域推广到复频域。
各个变换的公式汇总
FS
fT(t)=n=−∞∑+∞Fnejnω0tω0=T2π(1)Fn=T1∫−2T2TfT(t)e−jnω0tdtn=0,±1,±2,...(2)
FT
f(t)=2π1∫−∞+∞∫−∞+∞f(t)e−jωtdtejωtdωF(jw)=∫−∞+∞f(t)e−jωtdt(1)f(t)=2π1∫−∞+∞F(jw)ejωtdω(2)
DTFT
X(ejω)=F[x(n)]=n=−∞∑∞x(n)e−jωn(1)x(n)=F−[X(ejω)]=2π1∫−ππX(ejω)ejωndω(2)
DFS
X(k)=DFS[x(n)]=n=0∑N−1x(n)e−jN2πkn(1)x(n)=IDFS[X(k)]=N1k=0∑N−1X(k)ejN2πkn(2)
DFT
X(k)=DFT[x(n)]=n=0∑N−1x(n)WNknk=0,1,...,N−1=n=0∑N−1x(n)e−jN2πnkk=0,1,...,N−1(1)x(n)=IDFT[X(k)]=N1k=0∑N−1X(K)WN−knn=0,1,...,N−1=n=0∑N−1x(n)ejN2πknk=0,1,...,N−1(2)WN=e−jN2π
总结
-
FT的时域是连续的、即对象是x(t),而DFT的时域是离散的、即对象是x(n),但变换的结果在频域都是连续的;
-
DFT与DTFT都是对时域离散序列x(n)进行频域变换;
-
DTFT的结果在频域是连续的,但DFT的结果在频域是离散的;
-
FT/DTFT的频率是ejω⟶ω、即连续的,DFT的频率是ejN2πkn⟶ω=N2πk,怎么理解N2πk是频率呢?我们知道x(n)是由x(t)采样而来的,假设采样频率为fs且满足奈奎斯特采样定理,则采样后的频谱是周期的、未混叠的;
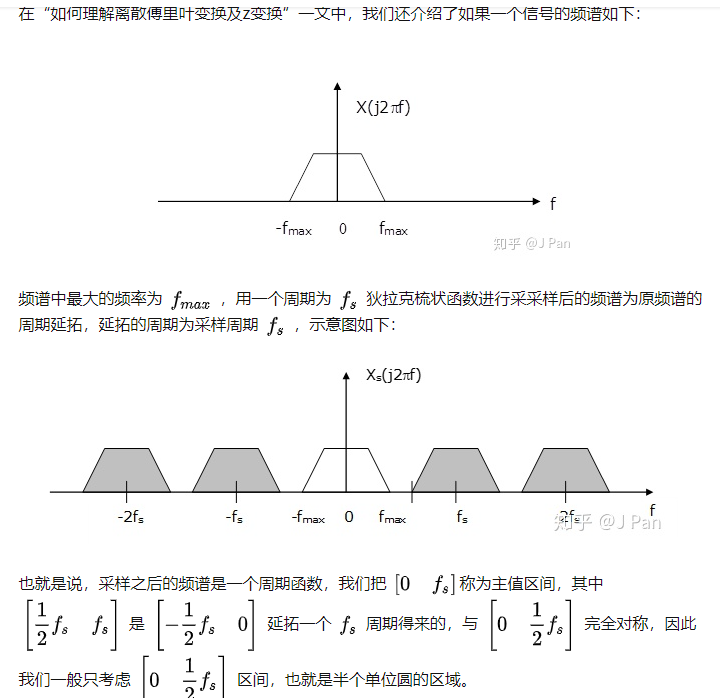
(0,π)对应着(0,0.5fs),因为(0,−π)和(0,π)是对称的,所以就不用看了。现在就可以求得DFT的频率了,即:
∵π0.5fs=N2πkωk∴ωk=π0.5fsN2πkk=0,1,...,N−1
-
x(n)是非周期的并且长度为N,我们对x(n)进行周期延拓得到x(n),x(n)的DFS的结果X(k)的主值序列等于x(n)的DFT的结果X(k)。


















